Ke – Cost of equity capital hay chi phí sử dụng vốn chủ sở hữu là một phần không thể thiếu trong chi phí sử dụng vốn bình quân WACC.
Ngoài ra, Ke còn được xem như thước đo để đánh giá tỷ suất sinh lời trên vốn chủ sở hữu ROE.
Theo đó:
- Nếu ROE > Ke chứng tỏ công ty đang hoạt động tương đối ổn định và ngày càng tạo ra nhiều giá trị cho cổ đông.
- Nếu ROE
Dù được sử dụng rất nhiều trong giới đầu tư, tuy nhiên cách tính Ke không hề đơn giản và phụ thuộc nhiều vào ý kiến chủ quan của người tính.
Tương tự, GoValue nhận được rất nhiều thắc mắc của các bạn trong việc toán toán các chỉ số Ke như thế nào?
Trong bài viết lần này hãy cùng GoValue tìm hiểu thật chi tiết về Ke, cũng như cách tiếp cận chỉ số này thông qua mô hình CAPM.
Nhưng trước hết, bạn đừng quên đọc bài nghiên cứu của GoValue về chi phí sử dụng vốn bình quân WACC.
Mô hình CAPM là gì?
Capital Asset Pricing Model (CAPM) là một mô hình thể hiện quan hệ giữa suất sinh lợi kỳ vọng của một tài sản, so với rủi ro của chính tài sản đó.
Kết quả của mô hình CAPM sẽ là tỷ lệ sinh lời yêu cầu của một tài sản (chi phí sử dụng vốn chủ – Ke).
Bằng cách so sánh tỷ lệ sinh lời yêu cầu, với khả năng sinh lời của vốn chủ sở hữu thực tế (ROE) chúng ta sẽ có cái nhìn sơ lược nhất về khả năng sinh lời của doanh nghiệp.
Nguyên tắc cơ bản ở đây là:
High risk – high return
Nếu bạn yêu cầu suất sinh lời của cổ phiếu càng lớn thì chi phí sử dụng vốn sẽ càng cao.
Nói cách khác, doanh nghiệp được lựa chọn sẽ càng khắt khe hơn.
Cách tính Ke theo mô hình CAPM
Chi phí sử dụng vốn Ke được tính theo công thức:
Trong đó:
- Rf: Lãi suất phi rủi ro (Risk free rate)
Lãi suất phi rủi ro là loại lãi suất mà tại đó, tỷ lệ rủi ro của tài sản gần bằng 0.
Thường thì lãi suất phi rủi ro sẽ được lấy bằng lãi suất trái phiếu chính phủ kỳ hạn 10 năm.
- Beta
Beta là đại được đo lường mức độ biến động của cổ phiếu so với thị trường chung.
- Risk premium = Rm – Rf
Risk premium là khoản thưởng khi bạn đầu tư vào cổ phiếu (rủi ro cao), so với cầm giữ các tài sản khác (có rủi ro thấp).
- Rm: Tỷ suất sinh lời yêu cầu (Required market return)
Ví dụ: Giả sử tỷ lệ phi rủi ro Rf = 5%, hệ số β = 0.84, thu nhập thị trường kỳ vọng là 15%, khi đó:
KE = 5% + 0.84 x (15% – 5%) = 13,4%
Tại sao thu nhập thị trường kỳ vọng lại là 15%?
Tính Beta = 0.84 như thế nào? Tại sao mỗi trang web lại cung cấp một chỉ số Beta khác nhau?
Đây là băn khoăn của rất nhiều bạn đã gửi tới GoValue, chúng ta sẽ đi vào chi tiết cách tính từng chỉ tiêu ngay sau đây.
Risk free rate (Rf) – Lãi suất phi rủi ro
Lãi suất phi rủi ro là lãi suất mà ở đó gần như rủi ro bằng 0.
Bên đi vay gần như chắc chắn sẽ trả được bạn tiền gốc cộng thêm một khoản lãi nhất định.
Bạn có thể lấy lãi suất trái phiếu chính phủ kỳ hạn 10 năm để làm lãi suất phi rủi ro.
Cập nhật thông tin chi tiết về lãi suất trái phiếu chính phủ tại đây.
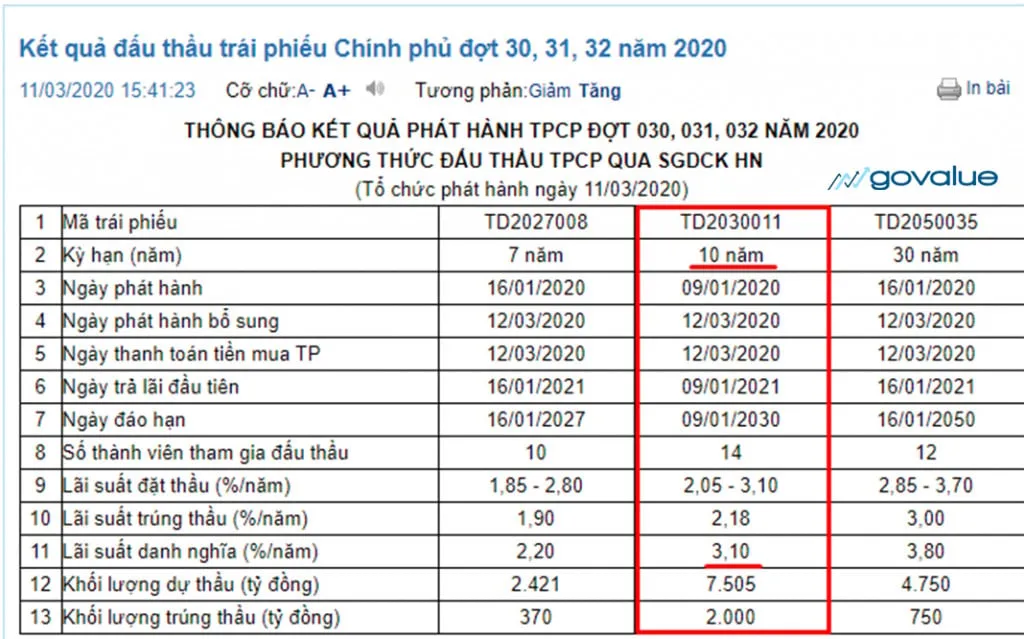
Bạn chú ý là chúng ta nên lấy danh nghĩa, bởi lãi suất trúng thầu sẽ biến động phụ thuộc nhiều vào kết quả đấu thầu của các ngân hàng thương mại.
Lãi suất danh nghĩa sẽ là khoản lãi suất thực mà Ngân hàng trung ương dùng để tính trái tức cho người nắm giữ.
Như vậy Lãi suất phi rủi ro trong thời điểm hiện tại (Tháng 3 – 2020) bằng 3,1%.
Hệ số Beta
Hệ số Beta là đại lượng đo lường mức độ rủi ro của cổ phiếu.
Có rất nhiều quan điểm về rủi ro nói chung của cổ phiếu, theo CAPM model thì rủi ro ở đây được hiểu là mức độ biến động của cổ phiếu so với thị trường chung.
Theo đó nếu Beta càng lớn, cổ phiếu sẽ biến động so với thị trường càng mạnh và đương nhiên cổ phiếu sẽ càng rủi ro.
Tuy nhiên, Warren Buffett lại cho rằng dùng Beta để do lường rủi ro của doanh nghiệp là rất “nực cười”…
Theo ông, rủi ro của cổ phiếu phải đi từ nội tại của doanh nghiệp.
Nếu giá cổ phiếu càng giảm sâu so với giá trị thực của cổ phiếu, khoản đầu tư này sẽ càng an toàn.
Bất kể chúng biến động ra sao.
Tuy nhiên Beta vẫn là chỉ số được rất nhiều bên chấp nhận. Trong bài viết lần này, chúng ta sẽ không bàn tới ai đúng, ai sai…
Trở lại với CAPM, một số mốc Beta đặc biệt bạn nên chú ý:
+ βi =1: Cổ phiếu biến thiên bằng thị trường, rủi ro bằng mức trung bình của thị trường.
Ví dụ khi chỉ số VNI tăng 1% thì cổ phiếu sẽ tăng 1%.
+ βi > 1: Rủi ro cao hơn mức trung bình của thị trường
Ví dụ Beta bằng = 1.2 khi chỉ số VNI tăng 1% thì cổ phiếu sẽ tăng 1.2%.
+ βi
Ví dụ Beta bằng = 0.5 khi chỉ số VNI tăng 1% thì cổ phiếu sẽ tăng 0.5%.
Cách tính chỉ số Beta
Như đã đề cập, Beta đo lường rủi ro bằng cách tính mức độ biến động của giá cổ phiếu với thị trường chung.
Nếu biểu diễn trên hình vẽ, Beta chính là hệ số góc đồ thị hàm số hồi quy tuyến tính của % thay đổi giá cổ phiếu (0y) theo % thay đổi chỉ số chung (Ox).
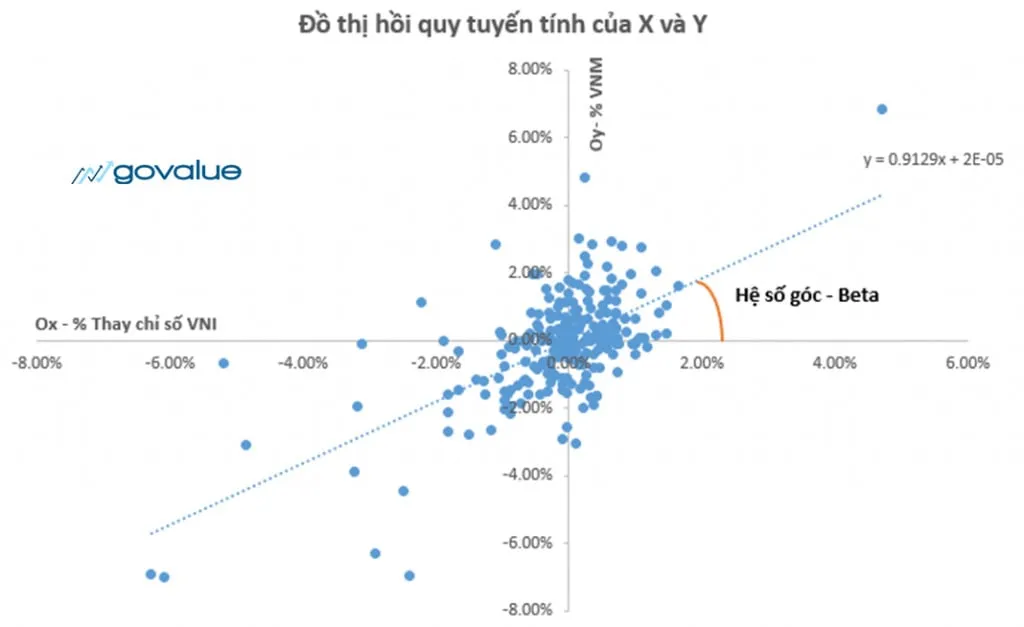
Nếu hệ số góc càng lớn thì Y sẽ biến động theo X càng lớn.
Lấy ví dụ về cổ phiếu Vinamilk, nếu biểu diễn phương trình đồ thị Y theo X trong 300 phiên giao dịch, ta sẽ có phương trình:
Y = 0.9129x + 2E – 0.5
Hệ số góc Beta = 0.9129, lúc này khi X (thị trường chung) thay đổi 1% thì Y (cổ phiếu VNM) sẽ thay đổi 0.9129%.
Có 2 cách để tính hệ số góc Beta này: Tự vẽ đồ thị bằng excel hoặc sử dụng hàm Slope có sẵn trong excel để tính hệ số góc.
Để tránh làm công việc trở nên phức tạp, GoValue sẽ chỉ trình bày cách tính nhanh hệ số góc Beta bằng hàm Slope trong khuôn khổ của bài viết này.
Tính Beta bằng cách sử dụng hàm Slope trong excel
Bước #1:
Tải dữ liệu về giá cổ phiếu và chỉ số VN-Index trên trang Investing.
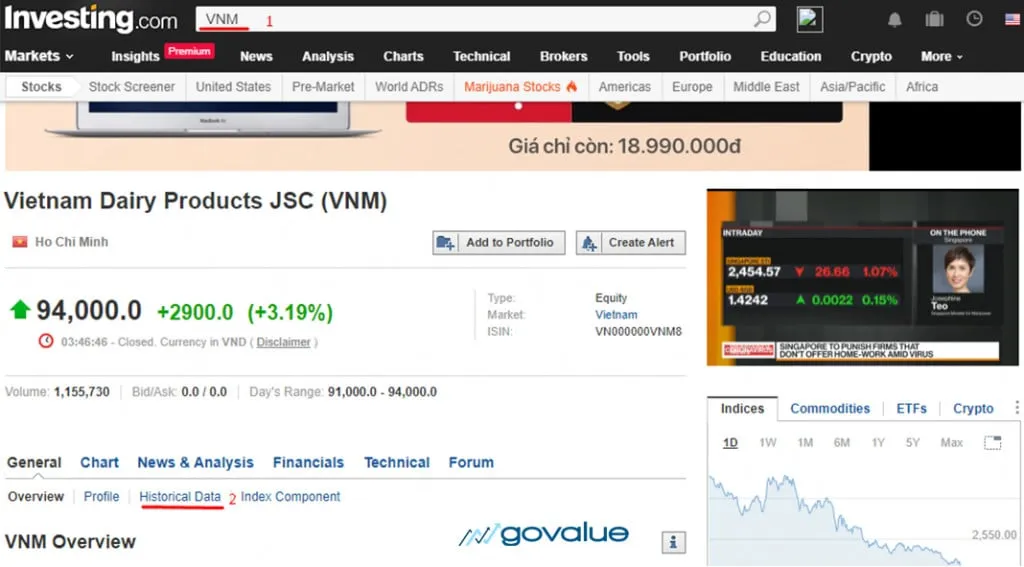
Bạn gõ mã cổ phiếu mình muốn tính và chọn Historical Data.
Bước #2: Nhập thời gian tương ứng (thường là 1 năm), chọn Apply và Download Data
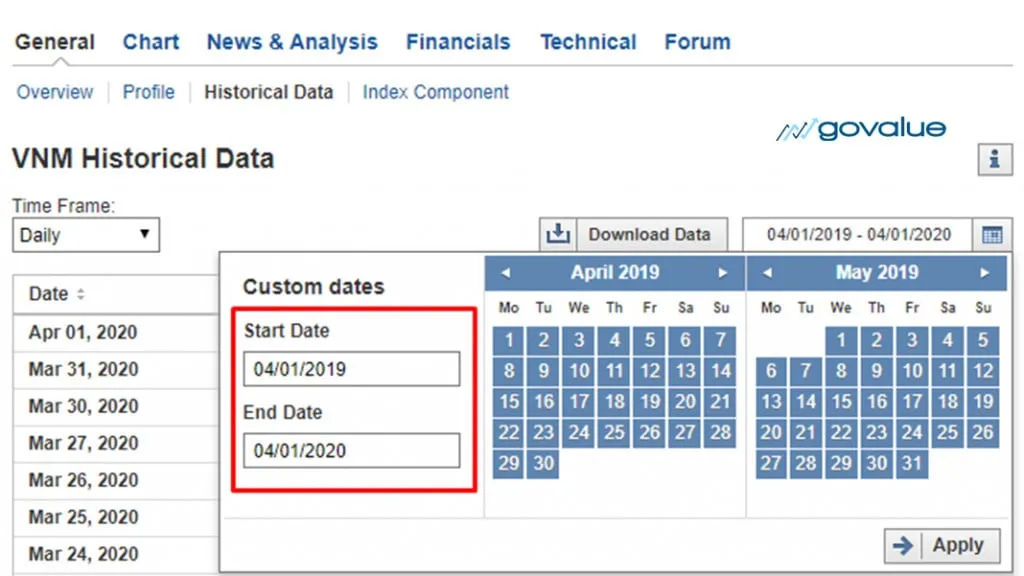
Bước #3: Làm tương tự với chỉ số VNI và copy cột “Change %” của 2 file excel vào cùng 1 sheet
Bước #4: Dùng hàm Slope để tính hệ số góc của hàm số
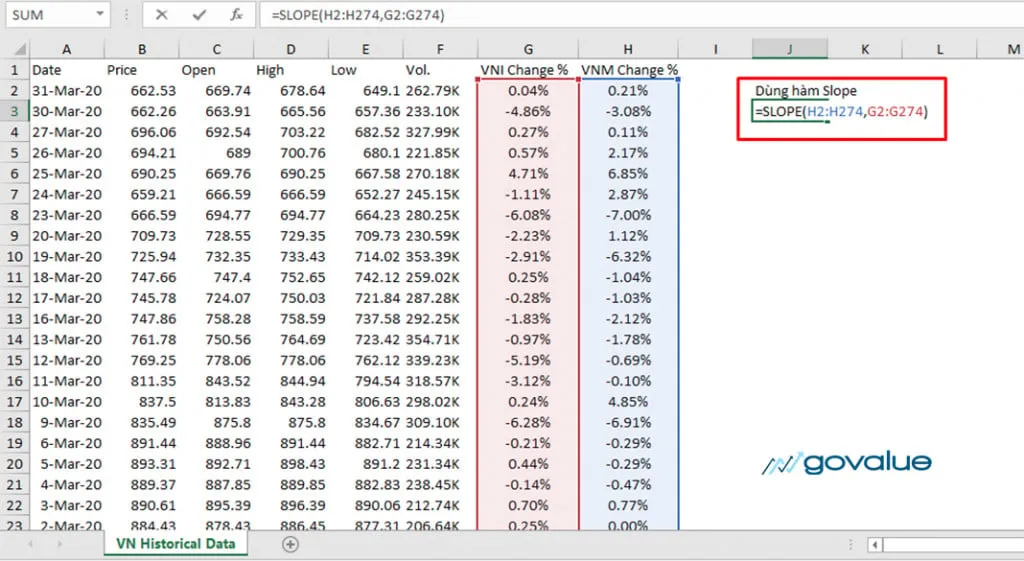
Kết quả trả về sẽ bằng 0.91 hay hệ số Beta = 0.91
Theo đó nếu chỉ số VNI tăng (giảm) 1% thì cổ phiếu VNM nhiều khả năng sẽ tăng (giảm) tương ứng 0.91%.
Trên một số trang cung cấp thông tin chứng khoán như Cafef, Vietstock,… cũng cung cấp sẵn chỉ số Beta của cổ phiếu.
Tuy nhiên do cách chọn mốc thời gian hoặc công thức tính khác nhau dẫn tới kết quả ra sẽ khác nhau.
Bạn có thể tự tính tay chỉ số Beta này để tăng độ chính xác của mô hình của mình.
Required market return (Rm)
Rm :Tỷ suất sinh lời kỳ vọng của thị trường
Thực sự, đây là phần dễ gây tranh cãi nhất trong mô hình CAPM.
Với mỗi nhà đầu tư khác nhau sẽ yêu cầu một mức sinh lời của thị trường khác nhau (Ví dụ: 15 – 20%)
Rất khó để xác định được đại lượng này.
Tuy nhiên, nếu bạn muốn một con số tương đối hợp lý để tính toán, tránh trường hợp đặt tùy tiện Rm…
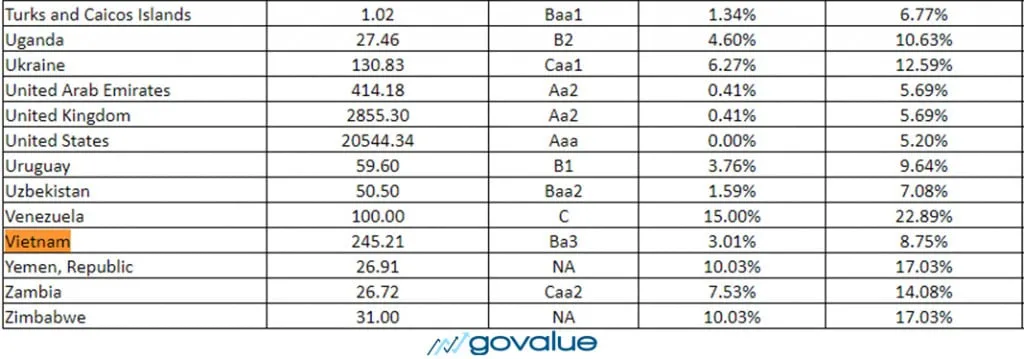
GoValue sẽ giới thiệu dữ liệu đã được giáo sư Damodaran tính sẵn.
Theo đó, bạn có thể lấy luôn phần Equity risk premium + rủi ro phi tài chính (Rf) để tính Required market return (Rm)
Hoặc tính bằng Total equity risk premium (kèm thêm phần Default spread) + rủi ro phi tài chính (Rf)
Bạn có thể cập nhật dữ liệu chi tiết Tại đây.
Với quan điểm thận trọng GoValue ưa thích cách thứ 2 hơn:
Rm = Total equity risk premium + Rf = 8.75% + 3.01% + 3.1% =14.86%
Vậy là chúng ta đã có đầy đủ các dữ kiện, cuối cùng là áp vào công thức tính Ke:
Ke = Rf +Beta*(Rm – Rf) = 3.1% + 0.91x(14.86% – 3.1%) = 13.8%
Như vậy là chúng ta đã biết cách tính Ke theo mô hình CAPM…
Là mô hình được sử dụng rất rộng rãi và đề cập tới nhiều yếu tố thị trường như Beta, lãi suất phi rủi ro,…
Qua đó phản ảnh rõ mối quan hệ giữa biến động của lãi suất và cơ hội đầu tư trong thực tế.
CAPM được xem như một phần quan trọng trong việc tính toán chi phí sử dụng vốn của doanh nghiệp.
Tuy nhiên không gì là hoàn hảo, CAPM cũng tồn tại một số điểm hạn chế nhất định sau.
Một số điểm hạn chế của mô hình CAPM
- Nhiều giả định phụ thuộc chủ quan vào người tính như Risk premium, mốc thời gian để tính Beta,…
- Dễ thay đổi ở những thời điểm định giá khác nhau.
- Tương đối khó tính đối với những bạn mới tham gia thị trường chứng khoán.
- Nhiều nghiên cứu trong thực tế đã chỉ ra CAPM còn nhiều bất cập, đôi khi là chưa chính xác.
Do đó, dù có được tính theo cách nào, sử dụng giả các dữ liệu có sẵn hay tự đặt cho mình lợi nhuận kỳ vọng riêng…
Điều quan trọng nhất vẫn là mức độ chịu đựng rủi ro, am hiểu doanh nghiệp của bạn.
Không nên áp dụng quá cứng nhắc các chỉ tiêu trong mô hình CAPM với toàn bộ doanh nghiệp.
