1. Yếu tố ảnh hưởng tới quyết định chọn cỡ mẫu
Kích thước mẫu (cỡ mẫu) của nghiên cứu càng lớn, sai số trong các ước lượng sẽ càng thấp, khả năng đại diện cho tổng thể càng cao. Tuy nhiên, việc thu thập cỡ mẫu lớn sẽ làm tiêu tốn nhiều thời gian, công sức, tiền bạc ở toàn bộ các khâu từ thu thập, kiểm tra, phân tích. Do đó việc chọn kích thước mẫu cần phải được xem xét một cách có cân nhắc để mọi thứ được cân bằng và hiệu quả. Sự lựa chọn cỡ mẫu sẽ phụ thuộc vào:
Bạn đang đọc: Các xác định kích thước mẫu trong nghiên cứu
- Độ tin cậy cần có của dữ liệu. Nghĩa là mức độ chắc chắn rằng các đặc điểm của cỡ mẫu được chọn phải khái quát được cho đặc điểm tổng thể.
- Sai số mà nghiên cứu có thể chấp nhận được. Đó là độ chính xác chúng ta yêu cầu cho bất ký ước lượng được thực hiện trên mẫu.
- Các loại kiểm định, phân tích sẽ thực hiện. Một số kỹ thuật thống kê yêu cầu cỡ mẫu phải đạt một ngưỡng nhất định thì các ước lượng mới có ý nghĩa.
- Kích thước của tổng thể. Mẫu nghiên cứu sẽ cần chiếm một tỷ lệ nhất định so với kích thước của tổng thể.

2. Xác định cỡ mẫu theo ước lượng tổng thể
Theo Yamane Taro (1967), việc xác định kích thước mẫu sẽ được chia làm hai trường hợp: không biết tổng thể và biết được tổng thể.
a. Trường hợp không biết quy mô tổng thể
Chúng ta sẽ sử dụng công thức sau:

Trong đó:
- n: kích thước mẫu cần xác định.
- Z: giá trị tra bảng phân phối Z dựa vào độ tin cậy lựa chọn. Thông thường, độ tin cậy được sử dụng là 95% tương ứng với Z = 1.96.
- p: tỷ lệ ước lượng cỡ mẫu n thành công. Thường chúng ta chọn p = 0.5 để tích số p(1-p) là lớn nhất, điều này đảm bảo an toàn cho mẫu n ước lượng.
- e: sai số cho phép. Thường ba tỷ lệ sai số hay sử dụng là: ±01 (1%), ±0.05 (5%), ±0.1 (10%), trong đó mức phổ biến nhất là ±0.05.
Ví dụ: Nghiên cứu sự hài lòng của khách hàng đã dùng sản phẩm nước giải khát Pepsi Cola tại TP.HCM. Đây là tổng thể không xác định được quy mô vì chúng ta không biết được có bao nhiêu khách hàng đã uống nước Pepsi Cola ở TP.HCM. Như vậy cỡ mẫu tối thiểu cần có của nghiên cứu sẽ là 385 người:
Tìm hiểu thêm: ANW LÀ GÌ? CÁC CỤM TỪ VIẾT TẮT THÔNG DỤNG TRONG TIN NHẮN TIẾNG ANH

b. Trường hợp biết quy mô tổng thể
Chúng ta sẽ sử dụng công thức sau:
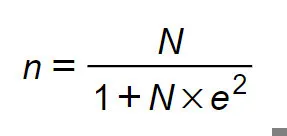
Trong đó:
- n: kích thước mẫu cần xác định.
- N: quy mô tổng thể.
- e: sai số cho phép. Thường ba tỷ lệ sai số hay sử dụng là: ±01 (1%), ±0.05 (5%), ±0.1 (10%), trong đó mức phổ biến nhất là ±0.05.
Ví dụ: Nghiên cứu sự hài lòng của khách hàng đã mua sữa bột Ensure Gold trong tháng 8 năm 2020 tại siêu thị Coopmart Phú Thọ (Quận 11, TP.HCM). Siêu thị tổng hợp danh sách khách hàng từ hệ thống thì có 1000 khách hàng, đây là tổng thể xác định được quy mô. Như vậy cỡ mẫu tối thiểu cần có của nghiên cứu nếu sai số e = ±0.05 sẽ là 286 người:
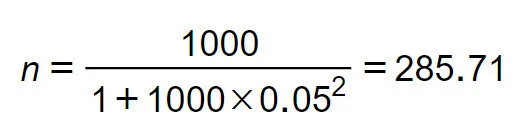
>>>>>Xem thêm: Gắn bi dương vật là gì? gắn bi có tốt không? Chi phí gắn bi bao nhiêu tiền?
3. Xác định cỡ mẫu theo ước lượng tổng thể
Việc xác định cỡ mẫu theo ước lượng tổng thể thường yêu cầu cỡ mẫu lớn. Tuy nhiên, nhà nghiên cứu lại có quỹ thời gian giới hạn và nếu không có nguồn tài chính tài trợ thì khả năng lấy mẫu theo ước lượng tổng thể sẽ khó có thể thực hiện. Do đó, các nhà nghiên cứu thường sử dụng công thức lấy mẫu dựa vào phương pháp định lượng được sử dụng để phân tích dữ liệu. Hai phương pháp yêu cầu cỡ mẫu lớn thường là hồi quy và phân tích nhân tố khám phá (EFA).
a. Kích thước mẫu theo EFA
Theo Hair và cộng sự (2014)[1], kích thước mẫu tối thiểu để sử dụng EFA là 50, tốt hơn là từ 100 trở lên. Tỷ lệ số quan sát trên một biến phân tích là 5:1 hoặc 10:1, một số nhà nghiên cứu cho rằng tỷ lệ này nên là 20:1. “Số quan sát” hiểu một cách đơn giản là số phiếu khảo sát hợp lệ cần thiết; “biến đo lường” là một câu hỏi đo lường trong bảng khảo sát. Ví dụ, nếu bảng khảo sát của chúng ta có 30 câu hỏi sử dụng thang đo Likert 5 mức độ (tương ứng với 30 biến quan sát thuộc các nhân tố khác nhau), 30 câu này được sử dụng để phân tích trong một lần EFA. Áp dụng tỷ lệ 5:1, cỡ mẫu tối thiểu sẽ là 30 × 5 = 150, nếu tỷ lệ 10:1 thì cỡ mẫu tối thiểu là là 30 × 5 = 300. Kích thước mẫu này lớn hơn kích thước tối thiểu 50 hoặc 100, vì vậy chúng ta cần cỡ mẫu tối thiểu để thực hiện phân tích nhân tố khám phá EFA là 150 hoặc 300 tùy tỷ lệ lựa chọn dựa trên khả năng có thể khảo sát được.
b. Kích thước mẫu theo hồi quy
Đối với kích thước mẫu tối thiểu cho phân tích hồi quy, Green (1991)[2] đưa ra hai trường hợp. Trường hợp một, nếu mục đích phép hồi quy chỉ đánh giá mức độ phù hợp tổng quát của mô hình như R2, kiểm định F … thì cỡ mẫu tối thiểu là 50 + 8m (m là số lượng biến độc lập hay còn gọi là predictor tham gia vào hồi quy). Trường hợp hai, nếu mục đích muốn đánh giá các yếu tố của từng biến độc lập như kiểm định t, hệ số hồi quy … thì cỡ mẫu tối thiểu nên là 104 + m (m là số lượng biến độc lập). Lưu ý rằng, m là số biến độc lập chúng ta đưa vào phân tích hồi quy, không phải là số biến quan sát hay số câu hỏi của nghiên cứu. Giả sử chúng ta xây dựng bảng khảo sát gồm 4 biến độc lập (4 thang đo), mỗi thang đo biến độc lập này được đo lường bằng 5 câu hỏi Likert (5 biến quan sát), như vậy tổng cộng chúng ta có 20 biến quan sát. Sau bước phân tích EFA, 4 thang đo này vẫn giữ nguyên như lý thuyết ban đầu, điều này đồng nghĩa có 4 biến độc lập sẽ được sử dụng cho phân tích hồi quy, tức m = 4 không phải m = 20.
Harris (1985)[3] cho rằng cỡ mẫu phù hợp để chạy hồi quy đa biến phải bằng số biến độc lập cộng thêm ít nhất là 50. Ví dụ, phép hồi quy có 4 biến độc lập tham gia, thì cỡ mẫu tối thiểu phải là 4 + 50 = 54. Hair và cộng sự (2014)[4] cho rằng cỡ mẫu tối thiểu nên theo tỷ lệ 5:1, tức là 5 quan sát cho một biến độc lập. Như vậy, nếu có 4 biến độc lập tham gia vào hồi quy, cỡ mẫu tối thiểu sẽ là 5 x 4 = 20. Tuy nhiên, 5:1 chỉ là cỡ mẫu tối thiểu cần đạt, để kết quả hồi quy có ý nghĩa thống kê cao hơn, cỡ mẫu lý tưởng nên theo tỷ lệ 10:1 hoặc 15:1. Riêng với trường hợp sử dụng phương pháp đưa biến vào lần lượt Stepwise trong hồi quy, cỡ mẫu nên theo tỷ lệ 50:1.
Nếu một bài nghiên cứu sử dụng kết hợp nhiều phương pháp xử lý thì sẽ lấy kích thước mẫu cần thiết lớn nhất trong các phương pháp. Ví dụ, nếu bài nghiên cứu vừa sử dụng phân tích EFA và vừa phân tích hồi quy. Kích thước mẫu cần thiết của EFA là 200, kích thước mẫu cần thiết của hồi quy là 100, chúng ta sẽ chọn kích thước mẫu cần thiết của nghiên cứu là 200 hoặc từ 200 trở lên. Thường chúng ta sử dụng phân tích EFA cùng với phân tích hồi quy trong cùng một bài luận văn, một bài nghiên cứu. EFA luôn đòi hỏi cỡ mẫu lớn hơn rất nhiều so với hồi quy, chính vì vậy chúng ta có thể sử dụng công thức tính kích thước mẫu tối thiểu cho EFA làm công thức tính kích thước mẫu cho nghiên cứu. Cũng lưu ý rằng, đây là cỡ mẫu tối thiểu, nếu chúng ta sử dụng cỡ mẫu lớn hơn kích thước tối thiểu, nghiên cứu sẽ càng có giá trị.
[1] Hair và cộng sự, Multivariate Data Analysis, Pearson, New Jersey, 2014.[2] Green & Salkind, Using SPSS for Windows and Macintosh: Analyzing and Understanding Data, Prentice Hall, New Jersey, 2003.
[3] Harris, A primer of multivariate statistics, New York: Academic Press,1985.
[4] Hair và cộng sự, Multivariate Data Analysis, Pearson, New Jersey, 2014.

